Forskel mellem T-test og ANOVA
 Share
Share
 Der er en tynd afgrænsningslinje midt i t-test og ANOVA, dvs. når populationen af kun to grupper skal sammenlignes, t-test bruges, men når midler fra mere end to grupper skal sammenlignes, ANOVA foretrækkes.
Der er en tynd afgrænsningslinje midt i t-test og ANOVA, dvs. når populationen af kun to grupper skal sammenlignes, t-test bruges, men når midler fra mere end to grupper skal sammenlignes, ANOVA foretrækkes.
T-test og variansanalyse forkortet som ANOVA er to parametriske statistiske teknikker, der bruges til at teste hypotesen. Da disse er baseret på den almindelige antagelse, ligesom den population, som prøven er trukket fra, skal normalt fordeles, homogenitet af varians, tilfældig sampling af data, observationer uafhængighed, måling af den afhængige variabel på forholdet eller intervalniveau, fortolker folk ofte disse to.
Her er en artikel præsenteret for dig for at forstå den betydelige forskel mellem t-test og ANOVA, se.
Indhold: T-test mod ANOVA
- Sammenligningstabel
- Definition
- Vigtige forskelle
- Konklusion
Sammenligningstabel
| Grundlag for sammenligning | T-test | ANOVA |
|---|---|---|
| Betyder | T-test er en hypotesetest, der bruges til at sammenligne middel fra to populationer. | ANOVA er en statistisk teknik, der bruges til at sammenligne middel fra mere end to populationer. |
| Teststatistik | (x ̄-µ) / (s / √n) | Mellem prøvevariation / Inden for prøvevarians |
Definition af T-test
T-testen beskrives som den statistiske test, der undersøger om populationsmidlerne for to prøver i høj grad adskiller sig fra hinanden ved hjælp af t-distribution, der bruges, når standardafvigelsen ikke er kendt, og prøvestørrelsen er lille. Det er et værktøj til at analysere, om de to prøver er trukket fra den samme population.
Testen er baseret på t-statistik, som antager, at variabel normalt er fordelt (symmetrisk klokkeformet fordeling), og gennemsnittet er kendt, og populationsvariansen beregnes ud fra prøven.
I t-test har nulhypotese form af H0: µ (x) = µ (y) mod alternativ hypotese H1: µ (x) ≠ µ (y), hvor µ (x) og µ (y) repræsenterer populationsmidlet. Graden af frihed for t-test er n1 + n2 - 2
Definition af ANOVA
Variansanalyse (ANOVA) er en statistisk metode, der ofte bruges i alle de situationer, hvor der skal foretages en sammenligning mellem mere end to populationsmidler som udbyttet af afgrøden fra flere frøvarianter. Det er et vigtigt værktøj til analyse for forskeren, der gør det muligt for ham at udføre test samtidig. Når vi bruger ANOVA, antages det, at prøven er trukket fra den normalt fordelte population og befolkningsvariansen er ens.
I ANOVA er den samlede variation af variation i et datasæt opdelt i to typer, dvs. det beløb, der er tildelt til chance og det beløb, der er tildelt til bestemte årsager. Dets grundlæggende princip er at teste variationerne mellem populationsmidler ved at vurdere variationen i gruppeposter i forhold til størrelsen af variationen mellem grupper. Inden i prøven er variansen på grund af den tilfældige uforklarlige forstyrrelse, hvorimod forskellige behandlinger kan forårsage mellem prøvevariansen.
Ved hjælp af denne teknik tester vi nulhypotese (H0) hvor alle populationsmidler er ens eller alternativ hypotese (H1) hvor mindst et populationsmiddel er forskelligt.
Nøgleforskelle mellem T-test og ANOVA
De væsentlige forskelle mellem T-test og ANOVA diskuteres detaljeret i de følgende punkter:
- En hypotetestest, der bruges til at sammenligne middel fra to populationer kaldes t-test. En statistisk teknik, der bruges til at sammenligne midlerne fra mere end to populationer er kendt som analyse af variation eller ANOVA.
- Teststatistik for T-test er:
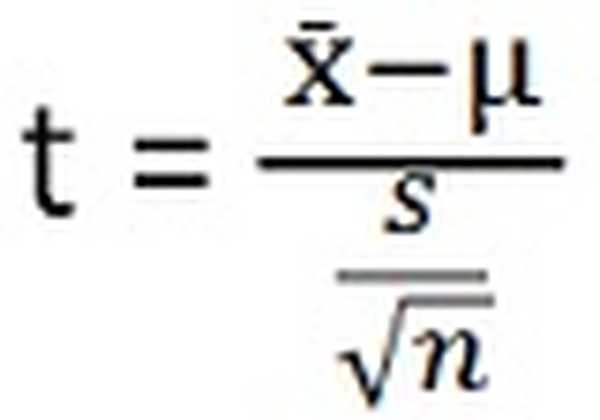 Teststatistik for ANOVA er:
Teststatistik for ANOVA er: 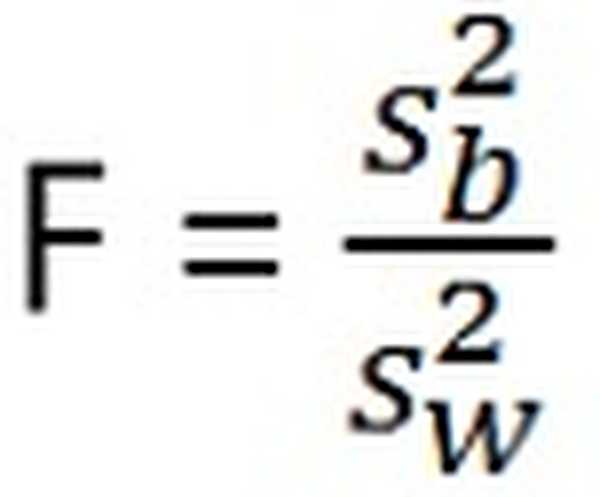
Konklusion
Efter gennemgang af ovenstående punkter kan det siges, at t-test er en speciel type ANOVA, der kan bruges, når vi kun har to populationer til at sammenligne deres midler. Selvom chancerne for fejl kan forøges, hvis der bruges t-test, når vi samtidig skal sammenligne mere end to midler til populationerne, er det derfor, ANOVA bruges
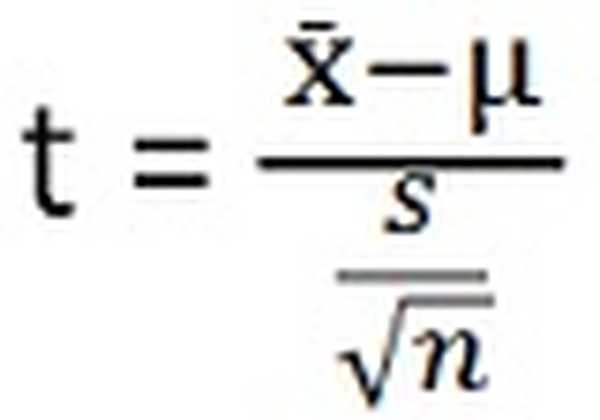 Teststatistik for ANOVA er:
Teststatistik for ANOVA er: